Research
Selected abstracts
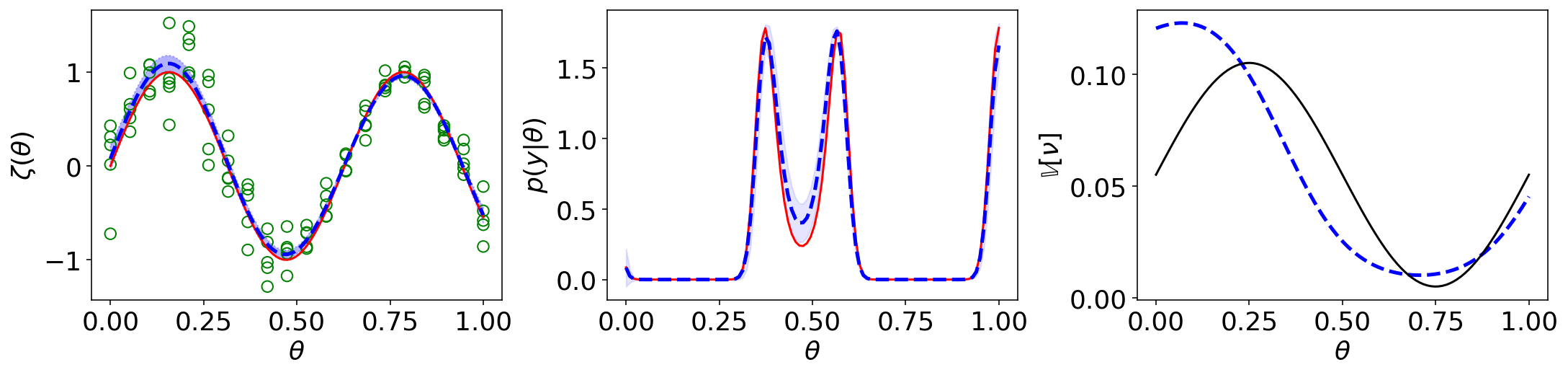
Calibration of expensive simulation models involves an emulator based on simulation outputs generated across various parameter settings to replace the actual model. Noisy outputs of stochastic simulation models require many simulation evaluations to understand the complex input-output relationship effectively. Sequential design with an intelligent data collection strategy can improve the efficiency of the calibration process. The growth of parallel computing environments can further enhance calibration efficiency by enabling simultaneous evaluation of the simulation model at a batch of parameters within a sequential design. This article proposes novel criteria that determine if a new batch of simulation evaluations should be assigned to existing parameter locations or unexplored ones to minimize the uncertainty of posterior prediction. Analysis of several simulated models and real-data experiments from epidemiology demonstrates that the proposed approach results in improved posterior predictions.
Özge Sürer.
Simulation models often have parameters as input and return outputs to understand the behavior of complex systems. Calibration is the process of estimating the values of the parameters in a simulation model in light of observed data from the system that is being simulated. When simulation models are expensive, emulators are built with simulation data as a computationally efficient approximation of an expensive model. An emulator then can be used to predict model outputs, instead of repeatedly running an expensive simulation model during the calibration process. Sequential design with an intelligent selection criterion can guide the process of collecting simulation data to build an emulator, making the calibration process more efficient and effective. This article proposes two novel criteria for sequentially acquiring new simulation data in an active learning setting by considering uncertainties on the posterior density of parameters. Analysis of several simulation experiments and real-data simulation experiments from epidemiology demonstrates that proposed approaches result in improved posterior and field predictions.
Özge Sürer.
Journal of Quality Technology (2024)
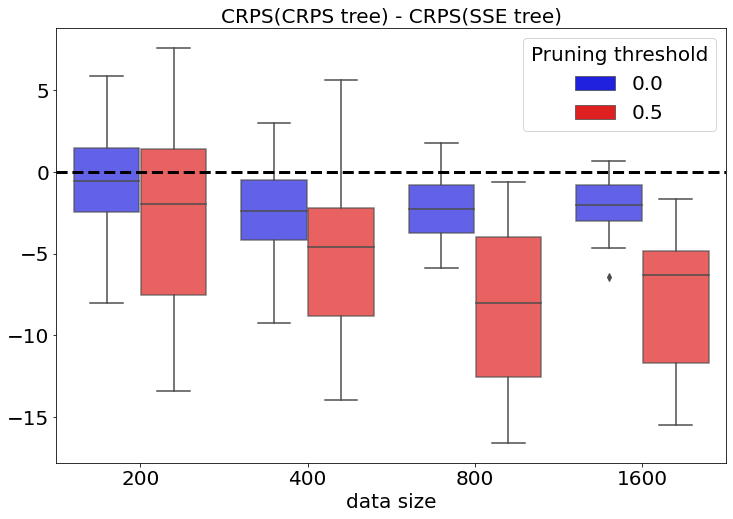
Decision trees built with data remain in widespread use for nonparametric prediction. Predicting probability distributions is preferred over point predictions when uncertainty plays a prominent role in analysis and decision-making. We study modifying a tree to produce nonparametric predictive distributions. We find the standard method for building trees may not result in good predictive distributions and propose changing the splitting criteria for trees to one based on proper scoring rules. Analysis of both simulated data and several real datasets demonstrates that using these new splitting criteria results in trees with improved predictive properties considering the entire predictive distribution.
Sara Shashaani, Özge Sürer, Matthew Plumlee, Seth Guikema.
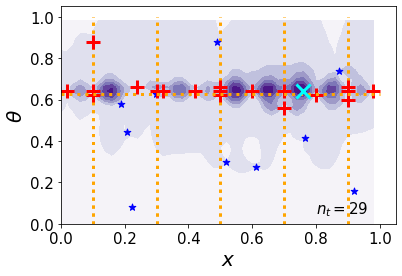
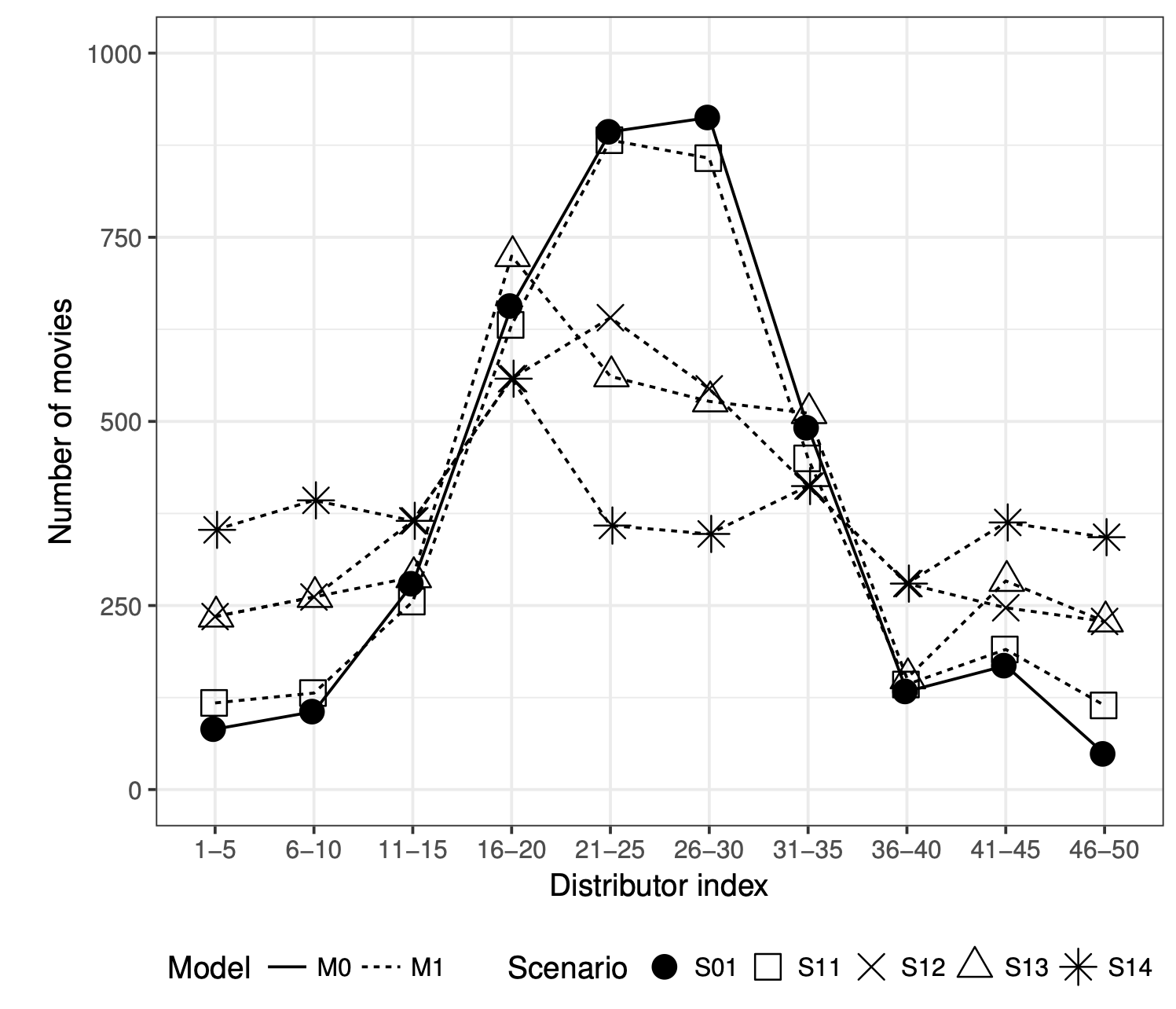
Simulation models of critical systems often have parameters that need to be calibrated using observed data. For expensive simulation models, calibration is done using an emulator of the simulation model built on simulation output at different parameter settings. Using intelligent and adaptive selection of parameters to build the emulator can drastically improve the efficiency of the calibration process. The article proposes a sequential framework with a novel criterion for parameter selection that targets learning the posterior density of the parameters. The emergent behavior from this criterion is that exploration happens by selecting parameters in uncertain posterior regions while simultaneously exploitation happens by selecting parameters in regions of high posterior density. The advantages of the proposed method are illustrated using several simulation experiments and a nuclear physics reaction model.
Özge Sürer, Matthew Plumlee, Stefan M. Wild.
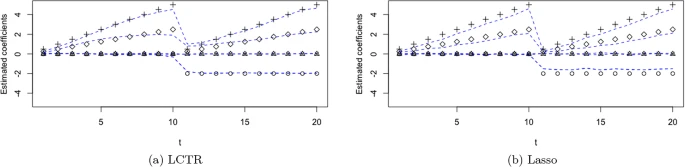
We consider the regression setting in which the response variable is not longitudinal (i.e., it is observed once for each case), but it is assumed to depend functionally on a set of predictors that are observed longitudinally, which is a specific form of functional predictors. In this situation, we often expect that the same predictor observed at nearby time points are more likely to be associated with the response in the same way. In such situations, we can exploit those aspects and discover groups of predictors that share the same (or similar) coefficient according to their temporal proximity. We propose a new algorithm called coefficient tree regression for data in which the non-longitudinal response depends on longitudinal predictors to efficiently discover the underlying temporal characteristics of the data. The approach results in a simple and highly interpretable tree structure from which the hierarchical relationships between groups of predictors that affect the response in a similar manner based on their temporal proximity can be observed, and we demonstrate with a real example that it can provide a clear and concise interpretation of the data. In numerical comparisons over a variety of examples, we show that our approach achieves substantially better predictive accuracy than existing competitors, most likely due to its inherent form of dimensionality reduction that is automatically discovered when fitting the model, in addition to having interpretability advantages and lower computational expense.
Özge Sürer, Daniel W. Apley, Edward C. Malthouse.
Advances in Data Analysis and Classification (2023)
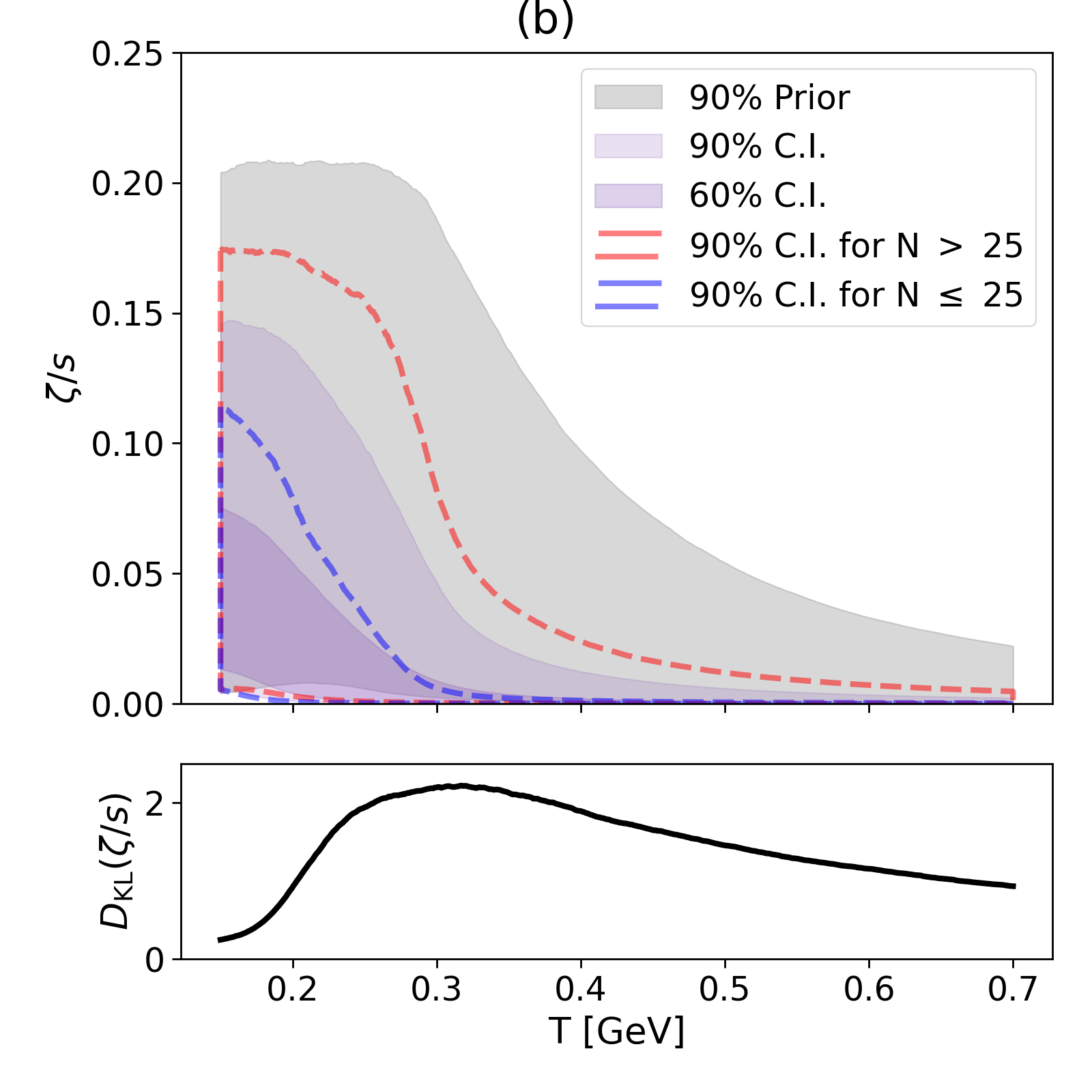
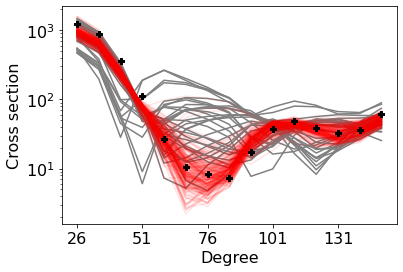
Due to large pressure gradients at early times, standard hydrodynamic model simulations of relativistic heavy-ion collisions do not become reliable until O(1)fm/c after the collision. To address this one often introduces a pre-hydrodynamic stage that models the early evolution microscopically, typically as a conformal, weakly interacting gas. In such an approach the transition from the pre-hydrodynamic to the hydrodynamic stage is discontinuous, introducing considerable theoretical model ambiguity. Alternatively, fluids with large anisotropic pressure gradients can be handled macroscopically using the recently developed Viscous Anisotropic Hydrodynamics (VAH). In high-energy heavy-ion collisions VAH is applicable already at very early times, and at later times transitions smoothly into conventional second-order viscous hydrodynamics (VH). We present a Bayesian calibration of the VAH model with experimental data for Pb–Pb collisions at the LHC. We find that the VAH model has the unique capability of constraining the specific viscosities of the QGP at higher temperatures than other previously used models.
Dananjaya Liyanage, Özge Sürer, Matthew Plumlee, Stefan M. Wild, Ulrich Heinz.
Due to large pressure gradients at early times, standard hydrodynamic model simulations of relativistic heavy-ion collisions do not become reliable until O(1)fm/c after the collision. To address this one often introduces a pre-hydrodynamic stage that models the early evolution microscopically, typically as a conformal, weakly interacting gas. In such an approach the transition from the pre-hydrodynamic to the hydrodynamic stage is discontinuous, introducing considerable theoretical model ambiguity. Alternatively, fluids with large anisotropic pressure gradients can be handled macroscopically using the recently developed Viscous Anisotropic Hydrodynamics (VAH). In high-energy heavy-ion collisions VAH is applicable already at very early times, and at later times transitions smoothly into conventional second-order viscous hydrodynamics (VH). We present a Bayesian calibration of the VAH model with experimental data for Pb–Pb collisions at the LHC. We find that the VAH model has the unique capability of constraining the specific viscosities of the QGP at higher temperatures than other previously used models.
Özge Sürer, Filomena M. Nunes, Matthew Plumlee, Stefan M. Wild.
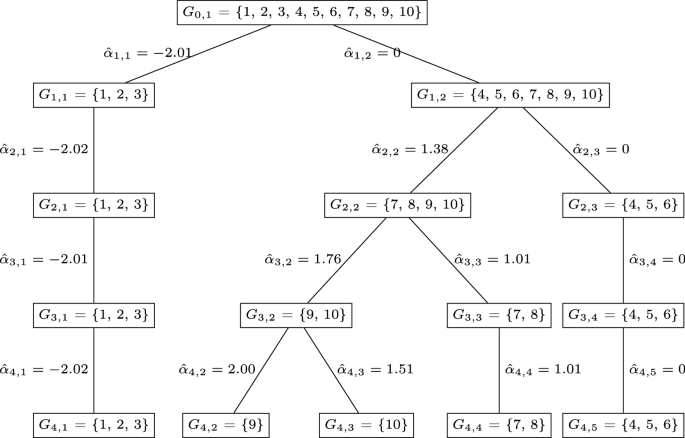
The proliferation of data collection technologies often results in large data sets with many observations and many variables. In practice, highly relevant engineered features are often groups of predictors that share a common regression coefficient (i.e., the predictors in the group affect the response only via their collective sum), where the groups are unknown in advance and must be discovered from the data. We propose an algorithm called coefficient tree regression (CTR) to discover the group structure and fit the resulting regression model. In this regard CTR is an automated way of engineering new features, each of which is the collective sum of the predictors within each group. The algorithm can be used when the number of variables is larger than, or smaller than, the number of observations. Creating new features that affect the response in a similar manner improves predictive modeling, especially in domains where the relationships between predictors are not known a priori. CTR borrows computational strategies from both linear regression (fast model updating when adding/modifying a feature in the model) and regression trees (fast partitioning to form and split groups) to achieve outstanding computational and predictive performance. Finding features that represent hidden groups of predictors (i.e., a hidden ontology) that impact the response only via their sum also has major interpretability advantages, which we demonstrate with a real data example of predicting political affiliations with television viewing habits. In numerical comparisons over a variety of examples, we demonstrate that both computational expense and predictive performance are far superior to existing methods that create features as groups of predictors. Moreover, CTR has overall predictive performance that is comparable to or slightly better than the regular lasso method, which we include as a reference benchmark for comparison even though it is non-group-based, in addition to having substantial computational and interpretive advantages over lasso.
Özge Sürer, Daniel W. Apley, Edward C. Malthouse.
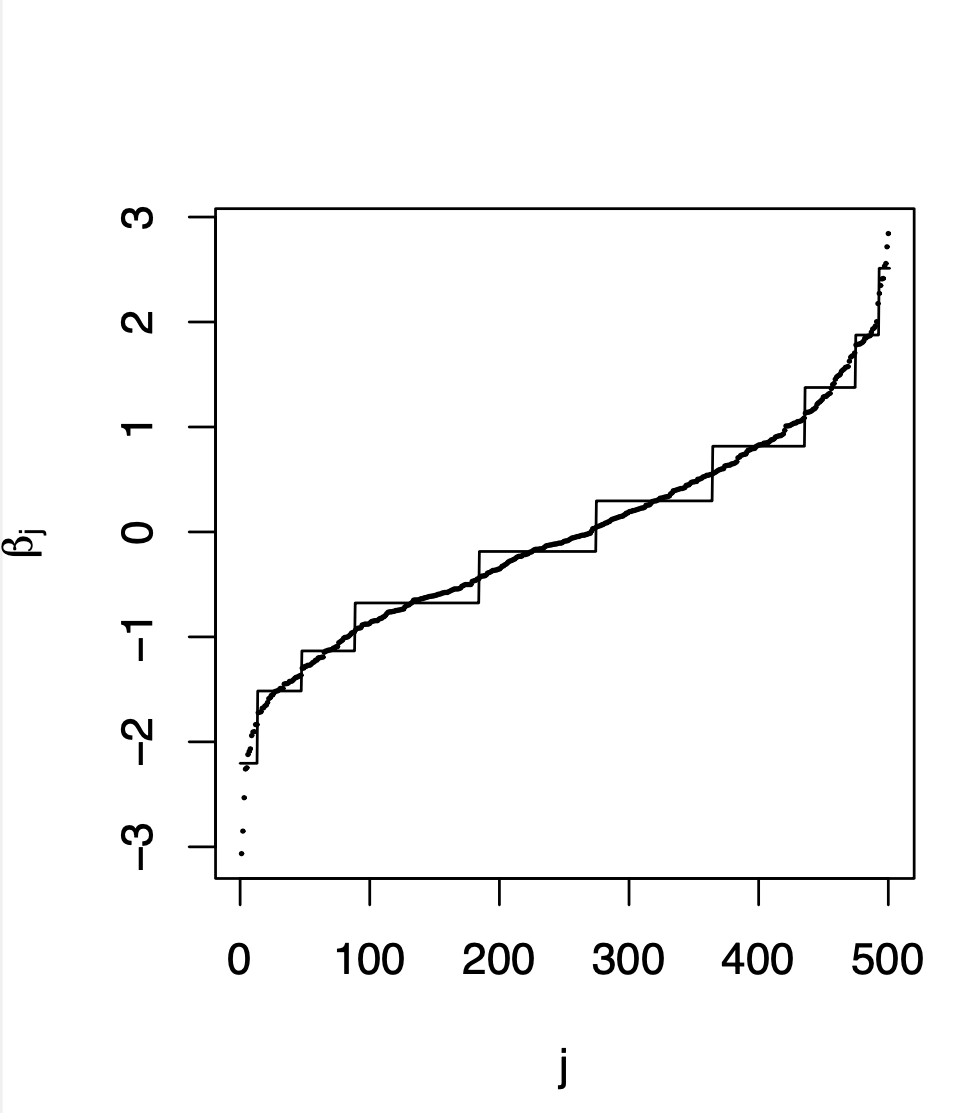
Large regression data sets are now commonplace, with so many predictors that they cannot or should not all be included individually. In practice, derived predictors are relevant as meaningful features or, at the very least, as a form of regularized approximation of the true coefficients. We consider derived predictors that are the sum of some groups of individual predictors, which is equivalent to predictors within a group sharing the same coefficient. However, the groups of predictors are usually not known in advance and must be discovered from the data. In this paper we develop a coefficient tree regression algorithm for generalized linear models to discover the group structure from the data. The approach results in simple and highly interpretable models, and we demonstrated with real examples that it can provide a clear and concise interpretation of the data. Via simulation studies under different scenarios we showed that our approach performs better than existing competitors in terms of computing time and predictive accuracy.
Özge Sürer, Daniel W. Apley, Edward C. Malthouse.
Statistical Analysis and Data Mining (2021)
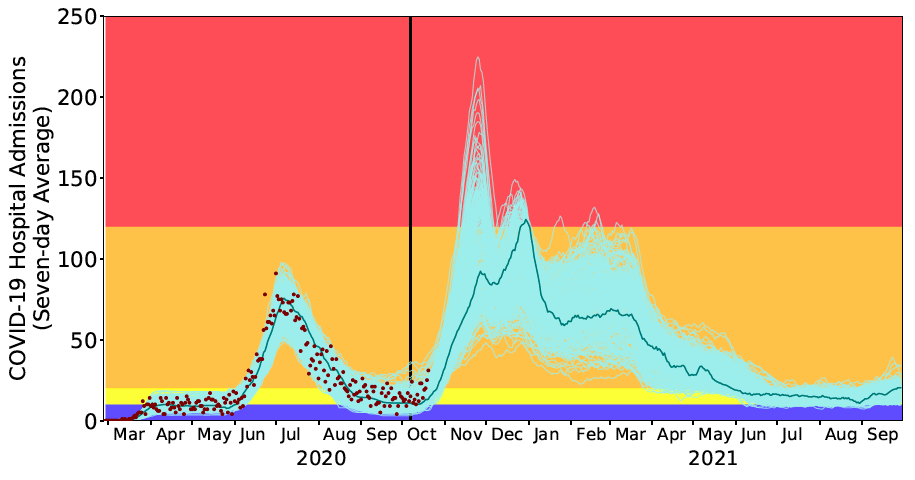
Community mitigation strategies to combat COVID-19, ranging from healthy hygiene to shelter-in-place orders, exact substantial socioeconomic costs. Judicious implementation and relaxation of restrictions amplify their public health benefits while reducing costs. We derive optimal strategies for toggling between mitigation stages using daily COVID-19 hospital admissions. With public compliance, the policy triggers ensure adequate intensive care unit capacity with high probability while minimizing the duration of strict mitigation measures. In comparison, we show that other sensible COVID-19 staging policies, including France’s ICU-based thresholds and a widely adopted indicator for reopening schools and businesses, require overly restrictive measures or trigger strict stages too late to avert catastrophic surges. As proof-of-concept, we describe the optimization and maintenance of the staged alert system that has guided COVID-19 policy in a large US city (Austin, Texas) since May 2020. As cities worldwide face future pandemic waves, our findings provide a robust strategy for tracking COVID-19 hospital admissions as an early indicator of hospital surges and enacting staged measures to ensure integrity of the health system, safety of the health workforce, and public confidence.
Haoxiang Yang, Özge Sürer, Daniel Duque, David Morton, Bismark Singh, Spencer Fox, Remy Pasco, Kelly Pierce, Paul Rathouz, Zhanwei Du, Michael Pignone, Mark E. Escott, Stephen I. Adler, Clairborne Johnston, Lauren Ancel Meyers.
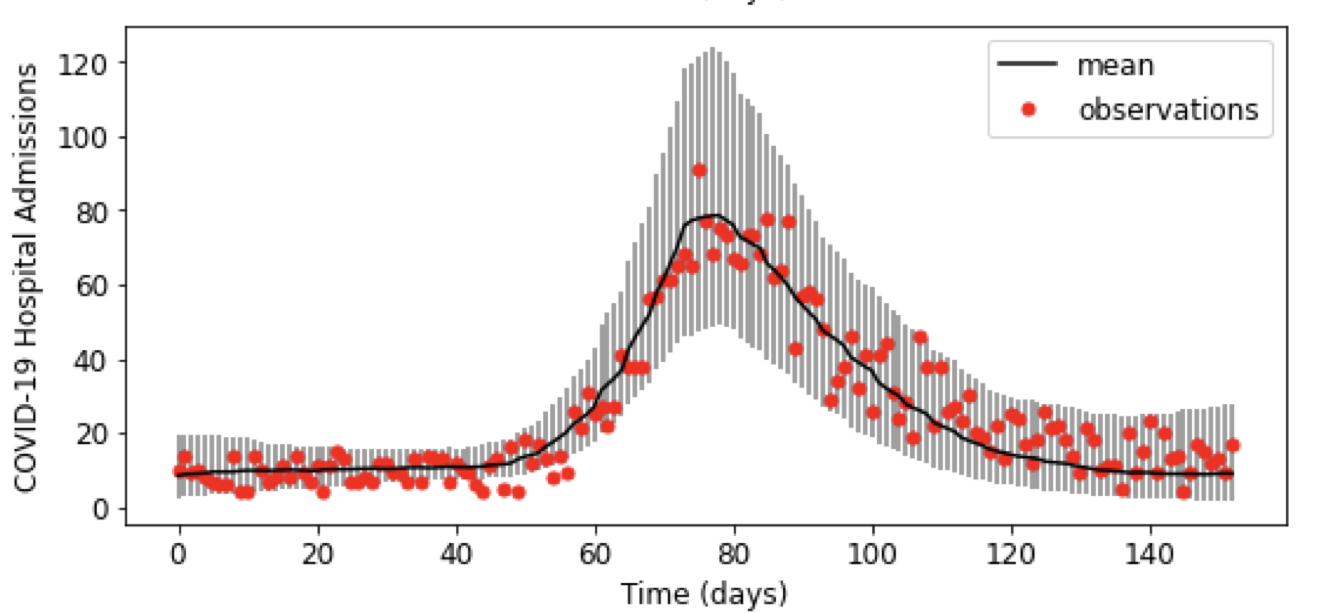
Calibration of parameters in simulation models is necessary to develop sharp predictions with quantified uncertainty. A scalable method for calibration involves building an emulator after conducting an experiment on the simulation model. However, when the parameter space is large, meaning the parameters are quite uncertain prior to calibration, much of the parameter space can produce unstable or unrealistic simulator responses that drastically differ from the observed data. One solution to this problem is to simply discard, or filter out, the parameters that gave unreasonable responses and then build an emulator only on the remaining simulator responses. In this article, we demonstrate the key mechanics for an approach that emulates filtered responses but also avoids unstable and incorrect inference. These ideas are illustrated on a real data example of calibrating COVID-19 epidemiological simulation model.
Özge Sürer, Matthew Plumlee.
Proceedings of Winter Simulation Conference (WSC) (2021)
Recommender systems are typically designed to optimize the utility of the end user. In many settings, however, the end user is not the only stakeholder and this exclusive focus may produce unsatisfactory results for other stakeholders. One such setting is found in multisided platforms, which bring together buyers and sellers. In such platforms, it may be necessary to jointly optimize the value for both buyers and sellers. This paper proposes a constraint-based integer programming optimization model, in which different sets of constraints are used to reflect the goals of the different stakeholders. This model is applied as a post-processing step, so it can easily be added onto an existing recommendation system to make it multi-stakeholder aware. For computational tractability with larger data sets, we reformulate the integer problem using the Lagrangian dual and use subgradient optimization. In experiments with two data sets, we evaluate empirically the interaction between the utilities of buyers and sellers and show that our approximation can achieve good upper and lower bounds in practical situations.
Özge Sürer, Robin Burke, Edward C. Malthouse.
Proceedings of the 12th ACM Conference on Recommender Systems (2018)
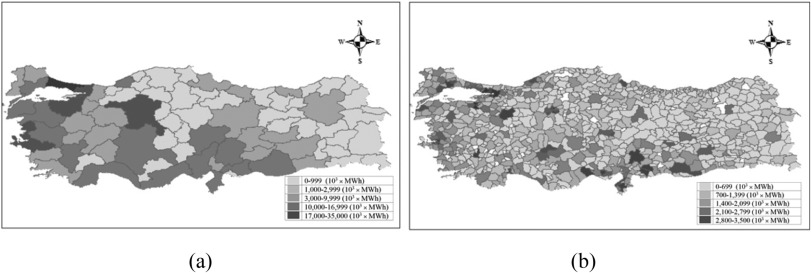
Geographical areas have diverse green energy resources and different levels of energy consumptions. An important challenge to satisfy the energy demand using green energy resources is to balance energy supply and demand. Territory design deals with the problem of grouping geographic areas into larger geographic clusters called territories in such a way that the grouping is acceptable according to a planning criterion. The aim of this study is to group geographic areas so that energy requirement in a geographic cluster matches the available green energy potential in the same cluster. In this way, investments may be supported through region specific policies. The problem is formulated as a mixed-integer linear programming model. A location-allocation approach is employed to solve the model. The location and allocation problems are solved iteratively. In order to solve the initial location problem, a Genetic Algorithm is developed to find the results of the p-median problem. Then, the allocation problem is solved optimally using the ILOG Cplex solver. The territory design problem is solved for Turkey and the results of various numbers of territories are compared. Among those trials, 10 territories result in the best balance of demand and supply.
Seda Yanik, Özge Sürer, Basar Oztaysi.
